nLab holographic entanglement entropy

Skip the Navigation Links | Home Page | All Pages | Latest Revisions | Discuss this page |
Redirected from "Ryu-Takayanagi formula".
Contents

Context

Quantum systems

quantum logic


quantum physics


quantum probability theory – observables and states


quantum information


quantum computation

qbit

quantum algorithms:


quantum sensing


quantum communication

Measure and probability theory

Contents

Idea

The term holographic entanglement entropy refers to expressions of entanglement entropy in boundary quantum field theories, via a version of AdS-CFT duality (“holography”), in terms of the geometry of a higher-dimensional bulk spacetime.

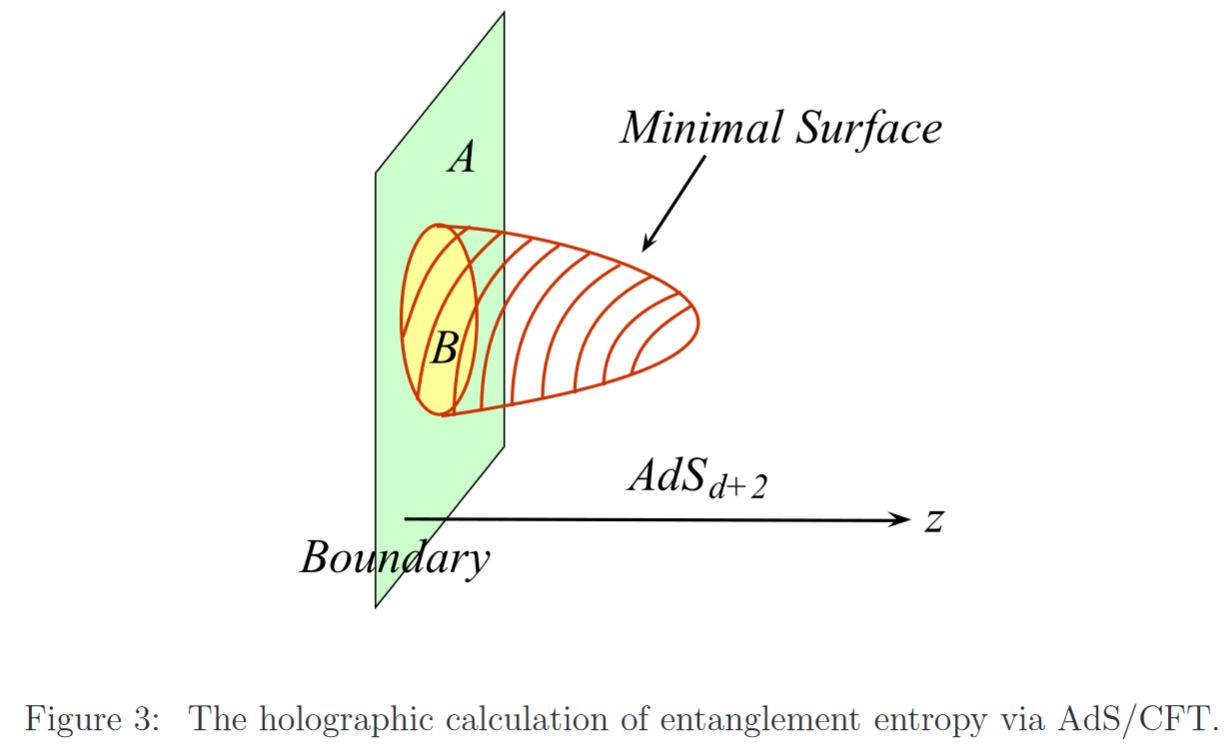
The essential idea is that the entanglement entropy of a region UU in the domain of a boundary field theory should be proportional to the volume (length, area, …) of the hypersurface Σ\Sigma in the bulk spacetime which shares the same boundary ∂U=∂Σ\partial U = \partial \Sigma and which has minimal volume with this property. A more precise version of this idea is given by the Ryu-Takayanagi formula, see below.

This kind of relation between entropy of quantum systems and area/volumes of critical surfaces in a curved spacetime is akin to the Bekenstein-Hawking entropy-formula for black holes, and indeed it is meant to subsume the black hole entropy-formula for black holes in anti de Sitter spacetimes.

While in the original context of the AdS-CFT correspondence the Ryu-Takayanagi formula remains ill-defined, or at least intractable in detail (not the least because it is, ultimately, a statement about non-perturbative string theory, hence about M-theory, which remains elusive), its general idea led to the discovery of fully well-defined discretized (“toy”) models of holography in terms of tensor networks that express (code subspaces) of quantum error correcting codes (such as the HaPPY code and Majorana dimer codes). In these holographic tensor network models the behaviour of holographic entanglement entropy, and of several other expected aspects of holography, turn out to have a faithful reflection (up to lattice effects caused by the discretization) amenable to explicit analysis, by tools

  1. from quantum information theory,

  2. from condensed matter physics (see also at AdS/CMT).

The power of these quantum information theory-methods in making precise and detailed sense of quantum gravity in a holographic bulk spacetime has re-inforced the earlier idea in AdS/CFT that notions of spacetime and of quantum gravity may be holographically defined and in fact emerge from non-gravitational quantum physics, and here specifically from quantum entanglement – an idea that has become known under the slogan “It from Qbit” (see also Georgescu 19). Just to keep in mind that, a priori, this applies “only” to the extra (higher) bulk dimensions of spacetime, while the definition of the boundary field theory typically relies on some notion domain space(-time) already (maybe unless one considers bulk duals of D(-1)-branes…).

Ryu-Takayanagi formula

For quantum field theories that are exhibited as boundary field theories on the asymptotic boundary AA of an approximately anti de Sitter spacetime via some approximation to AdS-CFT duality (for instance for QCD via AdS-QCD duality) their entanglement entropy of a given bounded domain B⊂AB\subset A turns out to be proportional to the volume (area) of the minimal-area codimension-2 hypersurface inside the bulk spacetime that has the same boundary ∂B\partial B (see Nishioka-Ryu-Takayanagi 09 (3.3) for review of the formula and Lewkowycz-Maldacena 13 for a conceptual explanation).

graphics grabbed from Nishioka-Ryu-Takayanagi 09

This relation is known as the Ryu-Takayanagi formula (Ryu-Takayanagi 06a, Ryu-Takayanagi 06b) for holographic computation of entanglement entropy, or holographic entanglement entropy, for short.

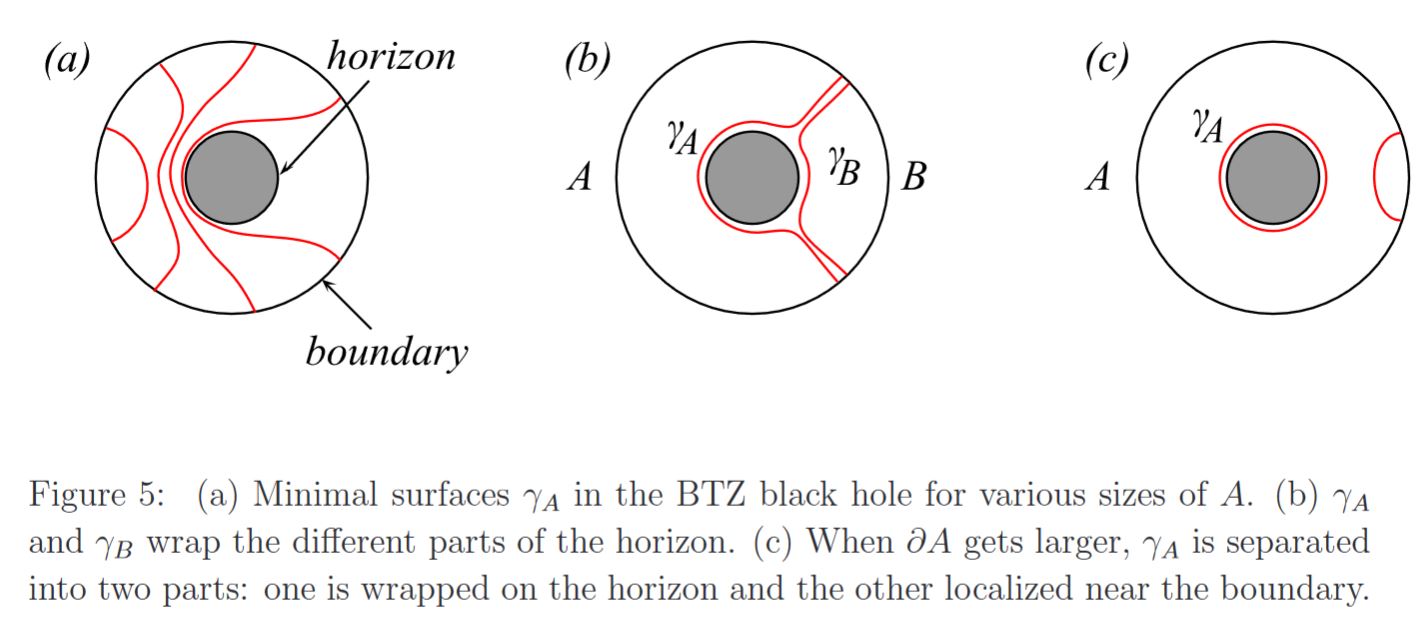
This is a generalization of the proportionality of black hole entropy to the area of its event horizon. Indeed, AdS-CFT duality applies to the near horizon geometry of black branes, the higher-dimensional generalizations of black holes and reduces 4d black holes under suitable KK-compactification (see also at black holes in string theory)

graphics grabbed from Nishioka-Ryu-Takayanagi 09

In fact quantum corrections to the black hole entropy in the presence of matter fields is equal to the entanglement entropy. (Ryu-Takayanagi 06a, p. 13)

Various properties of entanglement entropy find immediate geometric interpretations this way, for instance subadditivity

graphics grabbed from Nishioka-Ryu-Takayanagi 09

Tensor network models

Further discussion of implications of the Ryu-Takayanagi formula in van Raamsdonk 10 suggested that the logic may also be turned around: Instead of computing entanglement entropy of a given boundary field theory from known bulk geometry, conversely the bulk spacetime may be reconstructed from knowledge of the entanglement entropy of a boundary field theory.

Talking this perspective to the extreme suggests a description of bulk spacetimes entirely in terms of quantum information theory/entanglement-relations of a boundary QFT (“tensor networks”, Swingle 09, Swingle 12, and quantum error correction codes ADH 14, PYHP 15, HNQTWY 16, see Harlow 18, Jahn-Eisert 21 for review).

Here a tensor network Poincaré dual to a finite-stage hyperbolic tesselation of the hyperbolic plane is interpreted as a discretized model for a bulk spacetime with holographic quantum state on its asymptotic boundary being given by the string diagram-evaluation of the tensor network as a linear map to the tensor product of spaces corresonding to the edges crossing the boundary of the tesselation.

from Harlow 18

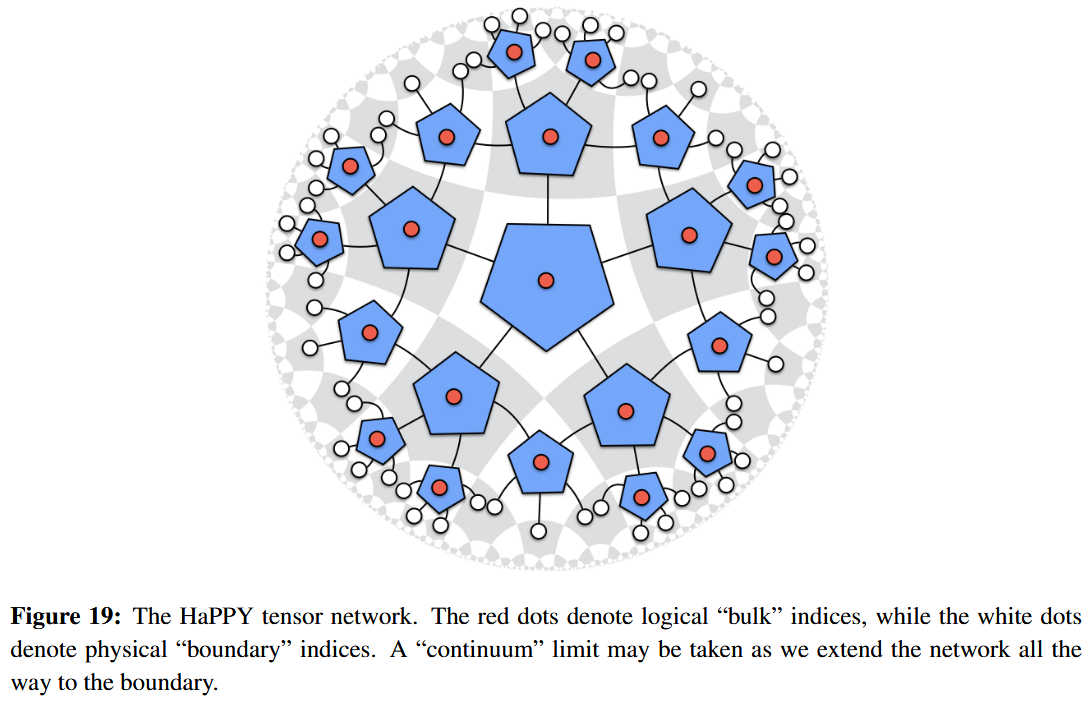
One shows (ADH 14) that this is a decent (“toy”) model of expected properties of bulk/boundary holography if this tensor network gives the code subspace of a quantum error correcting code.

For example, the tensor network corresponding to the pentagonal {5,4}\{5,4\} tesselation with a perfect tensor of rank 5+15+1 assigned to each tile yields a quantum error correcting code now known as the HaPPY code.

The idea is that the code subspace of this HaPPY code is that subspace of the boundary space of quantum states which holographically corresponds to all bulk states without a black hole in the bulk.

From Jahn Eisert 21

More generally, deleting any of the tiles in the interior of the tesselation is interpreted as the appearance of a bulk black hole, whose Bekenstein-Hawking entropy is carried by the quantum states carried by the loose edges that cross over the “event horizon” to the now deleted tiles.

The extreme case that all tiles are deleted from the tensor network, is thus interpreted describing a black hole that has swallowed up the entire bulk spacetime such that its horizon now coincides with the previous asymptotic boundary, whence its quantum states and entropy now coincide with that of the holographic boundary theory.


In this discrete HaPPY code model for the AdS-CFT correspondence the Ryu-Takayanagi formula for holographic entanglement entropy (above) has an exact proof PYHP 15, Theorem 2.

Chord diagram representation

In fact, holographic entanglement entropy in the HaPPY code turns out to be entirely encoded by the dimer network in the underlying Majorana dimer code (JGPE 19):

From JGPE 19

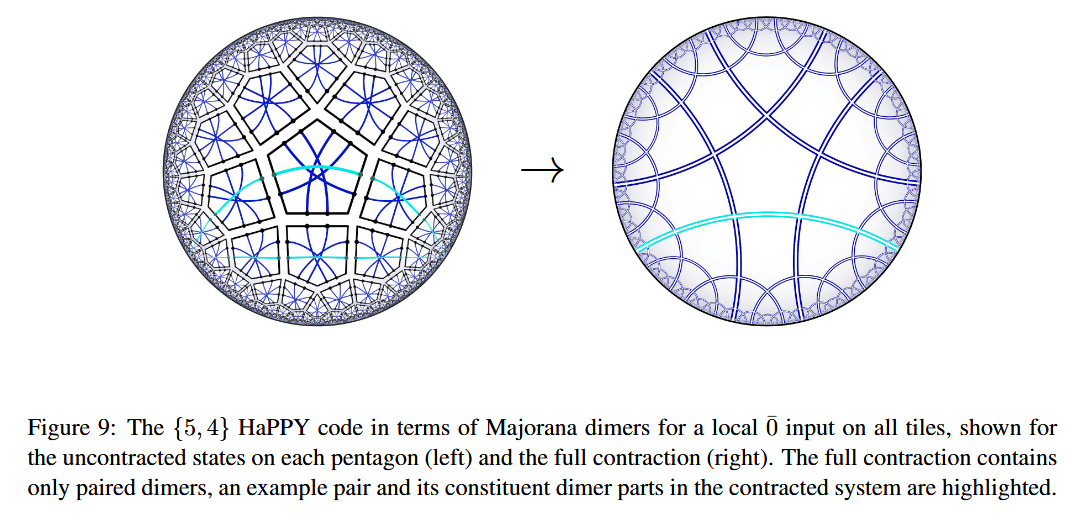
in that the entanglement entropy S AS_A of any Majorana dimer code-tensor network state turns out to count the number of dimers that cross between the (connected) subregion AA and its complement:

From JGPE 19
From Yan 20

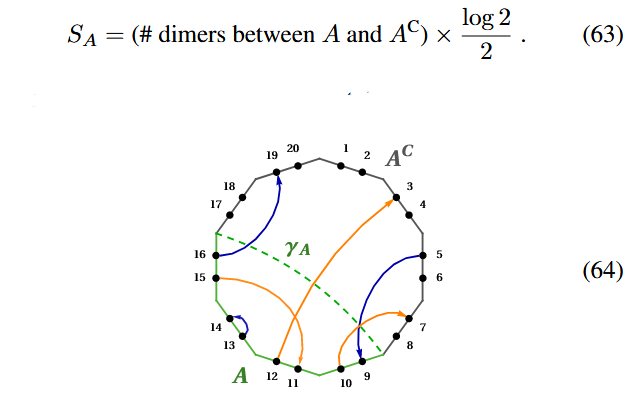
In the case that the dimers correspond to the hyperbolic tesselation {5,4}\{5,4\} from the HaPPY code, this entropy formula

S A=12ln(2 |Chords(A,A¯)|) S_A \;=\; \tfrac{1}{2} \ln \big( 2^{ \left\vert Chords(A, \bar A) \right\vert } \big)

recovers the Ryu-Takayanagi formula (JGPE 19 (78)), as here the number of chords crossing any hyperbolic geodesic grows linearly with the length of this geodesic.

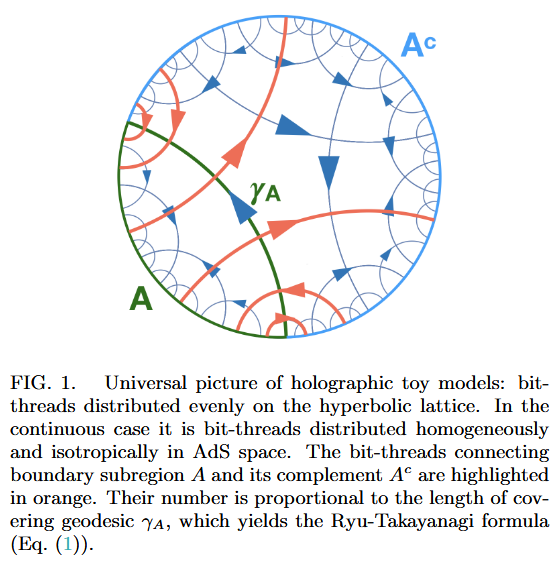
In the continuum limit this says that holographic entanglement entropy is exhibited by the geodesic flow out of the given subregion through its corresponding minimal bulk surface, an idea that was previously proposed in “bit-thread models” for holographic entanglement entropy (Freedman & Headrick 16):

from Freedman Headrick 16
from Sati Schreiber 19c

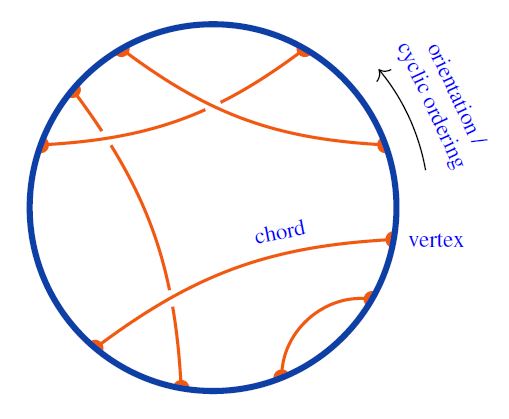
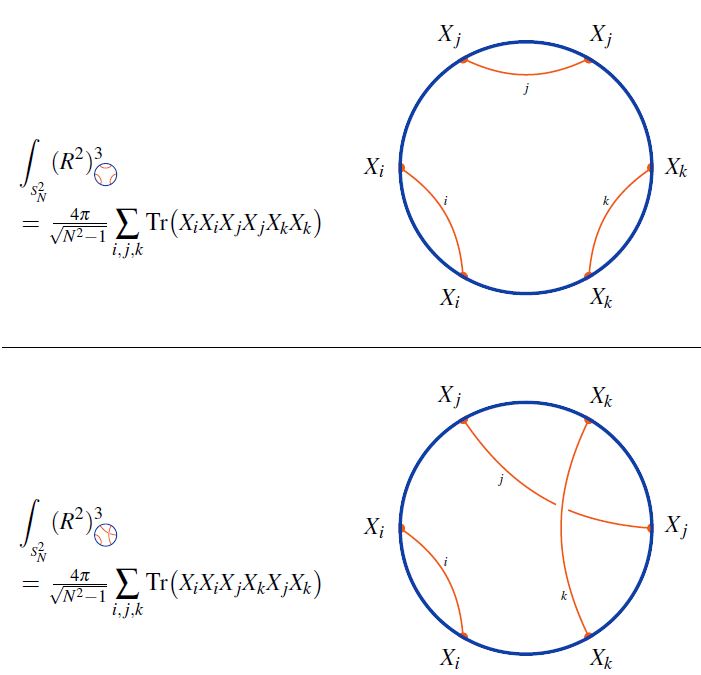
Following Sati-Schreiber 19c we recognize the above Majorana dimer/bit-thread networks from JGPE 19, Yan 19 as chord diagram-encodings of holographic bulks (p. 38).

Notice how each chord here reflects at the same time

  1. one entangled pair of qbits in the boundary quantum system;

  2. a geodesic through the hyperbolic plane bulk spacetime.

This is a (rigorous) state of affairs reminiscent of the “ER = EPR” slogan.


References

General

The original articles are

A proposal for a conceptual explanation:

Review:

Textbook account:

Survey talks:

  • Robert Myers, Holographic entanglement entropy, (pdf slides)

  • Shinsei Ryu, Holographic geometry in Entanglement Renormalization (pdf slides)

  • Juan Jottar, (Entanglement) Entropy in three-dimensional higher spin theories (pdf slides)

  • Matthew Headrick, Entanglement entropies in holographic field theory (pdf slides)

  • Tom Hartmann, Entanglement entropy and geometry, talk slides, 2014 (pdf)

An influential argument that this relation implies that entanglement in the boundary theory is what makes spacetime as such appear in the bulk theory is due to

reviewed in

  • Mark Van Raamsdonk, Lectures on Gravity and Entanglement, chapter 5 in New Frontiers in Fields and Strings

    TASI 2015 Proceedings of the 2015 Theoretical Advanced Study Institute in Elementary Particle Physics 2015 Theoretical Advanced Study Institute in Elementary Particle Physics (arXiv:1609.00026)

Discussion of the corresponding continuum theory, formulated via local nets of observables in algebraic quantum field theory:

See also:

  • Matthew Headrick, Veronika E. Hubeny, Covariant bit threads [arXiv:2208.10507]

  • Eugenia Colafranceschi, Xi Dong, Donald Marolf, Zhencheng Wang, Algebras and Hilbert spaces from gravitational path integrals: Understanding Ryu-Takayanagi/HRT as entropy without invoking holography [arXiv:2310.02189]

Via holographic tensor networks and quantum codes

Relation to renormalization of entanglement and tensor networks is due to

and further in terms of quantum error correcting codes due to

reviewed in

See also

Further development of these tensor networks:

The bit-thread proposal for associating holographic entanglement entropy with geodesic flow in hyperbolic space:

Embedding of the HaPPY code and the bit-thread models in more general Majorana dimer codes:

reviewed in:

See also:

Computation of black hole entropy in 4d via AdS4-CFT3 duality from holographic entanglement entropy in the ABJM theory for the M2-brane is discussed in

  • Jun Nian, Xinyu Zhang, Entanglement Entropy of ABJM Theory and Entropy of Topological Black Hole (arXiv:1705.01896)

Discussion in terms of DHR superselection theory:

  • Horacio Casini, Marina Huerta, Javier M. Magan, Diego Pontello, Entanglement entropy and superselection sectors I. Global symmetries (arXiv:1905.10487)

Discussion of gauge symmetry of holographic tensor networks and their quantum error correcting codes:

  • Kfir Dolev, Vladimir Calvera, Sam Cree, Dominic J. Williamson, Gauging the bulk: generalized gauging maps and holographic codes (arXiv:2108.11402)

In relation to renormalization group flow:

  • Keiichiro Furuya, Nima Lashkari, Mudassir Moosa, Renormalization group and approximate error correction (arXiv:2112.05099)

Musings on possible implications on relations between quantum gravity and quantum information:

Wilson lines computing holographic entropy in AdS 3/CFT 2AdS_3/CFT_2

Discussion of BTZ black hole entropy and more generally of holographic entanglement entropy in 3d quantum gravity/AdS3/CFT2 via Wilson line observables in Chern-Simons theory:

  • Martin Ammon, Alejandra Castro, Nabil Iqbal, Wilson Lines and Entanglement Entropy in Higher Spin Gravity, JHEP 10 (2013) 110 (arXiv:1306.4338)

  • Jan de Boer, Juan I. Jottar, Entanglement Entropy and Higher Spin Holography in AdS 3AdS_3, JHEP 1404:089, 2014 (arXiv:1306.4347)

  • Alejandra Castro, Stephane Detournay, Nabil Iqbal, Eric Perlmutter, Holographic entanglement entropy and gravitational anomalies, JHEP 07 (2014) 114 (arXiv:1405.2792)

  • Mert Besken, Ashwin Hegde, Eliot Hijano, Per Kraus, Holographic conformal blocks from interacting Wilson lines, JHEP 08 (2016) 099 (arXiv:1603.07317)

  • Andreas Blommaert, Thomas G. Mertens, Henri Verschelde, The Schwarzian Theory - A Wilson Line Perspective, JHEP 1812 (2018) 022 (arXiv:1806.07765)

  • Ashwin Dushyantha Hegde, Role of Wilson Lines in 3D Quantum Gravity, 2019 (spire:1763572)

  • Xing Huang, Chen-Te Ma, Hongfei Shu, Quantum Correction of the Wilson Line and Entanglement Entropy in the AdS 3AdS_3 Chern-Simons Gravity Theory (arXiv:1911.03841)

  • Eric D'Hoker, Per Kraus, Gravitational Wilson lines in AdS 3AdS_3 (arXiv:1912.02750)

  • Marc Henneaux, Wout Merbis, Arash Ranjbar, Asymptotic dynamics of AdS 3AdS_3 gravity with two asymptotic regions (arXiv:1912.09465)

and similarly for 3d flat-space holography:

Discussion for 3d de Sitter spacetime:

  • Alejandra Castro, Philippe Sabella-Garnier, Claire Zukowski, Gravitational Wilson Lines in 3D de Sitter (arXiv:2001.09998)

Application to AdS/QCD

Application to AdS/QCD:

  • Zhibin Li, Kun Xu, Mei Huang, The entanglement properties of holographic QCD model with a critical end point (arXiv:2002.08650)

Entanglement island proposal for BH information paradox

Claims

Claim that the proper application of holographic entanglement entropy to the discussion of Bekenstein-Hawking entropy resolves the apparent black hole information paradox:

Review aimed at readers with minimal background:

See also:

Criticism

  • Anna Karlsson, Concerns about the replica wormhole derivation of the island conjecture (arXiv:2101.05879)

  • Harvendra Singh, Islands and Icebergs contribute nothing to the Page curve (System with a symmetrical bath) [arXiv:2210.13970]

Argument that the would-be proof of the island conjecture secretly works only for massive gravity:

reviewed in:

  • Hao Geng, Recent Progress in Quantum Gravity: Karch-Randall Braneworld, Entanglement Islands and Graviton Mass, Washington (2022) [hdl:1773/49427]

and discussion of what to do about this problem:

Claim that the whole argument relies on the false assumption that the split property holds for quantum gravity:

Review in:

  • Nirmalya Kajuri, Of Islands, Holograms and Saving Quantum Physics From a Black Hole Paradox, Science – The Wire (Nov 2022)

    […][\ldots] a few sceptics have argued that while the calculations are correct, they don’t help resolve the black hole information-loss paradox. The troubles stem from the reservoir attached to the anti-de Sitter universe. The physicists who authored the island papers assumed that gravity stopped at the boundary of the anti-de Sitter space and didn’t enter the reservoir. This is not an innocuous assumption. […][\ldots] The key takeaway is that the island way to recover information and save unitarity works perfectly well – if you slightly modify Einstein’s theory of gravity. These criticisms have been around for some two years now, and physicists are yet to resolve them in print. […][\ldots] physicists continue to publish papers by the hundreds about the entanglement islands but few attempt to answer whether the islands are compatible with the Einsteinian gravity of our universe. […][\ldots]

See also:

  • Saskia Demulder, Alessandra Gnecchi, Ioannis Lavdas, Dieter Lüst, Islands and Light Gravitons in type IIB String Theory [arXiv:2204.03669]

  • Emil Martinec: “Thus far, picturesque evocations of quantum wormholes remain largely just that – picturesque evocations.” (2nd Nov 2022)

Argument that discussion of the issue in the toy example of 2d JT gravity does not actually generalize to higher dimensions:

  • Filip Landgren, Arvind Shekar, Islands and entanglement entropy in dd-dimensional curved backgrounds [arXiv:2401.01653]

Debate between a proponent and a critic :

See also:

Chord diagrams and weight systems in Physics

The following is a list of references that involve (weight systems on) chord diagrams/Jacobi diagrams in physics:

  1. In Chern-Simons theory

  2. In Dp-D(p+2) brane intersections

  3. In quantum many body models for for holographic brane/bulk correspondence:

    1. In AdS2/CFT1, JT-gravity/SYK-model

    2. As dimer/bit thread codes for holographic entanglement entropy

For a unifying perspective (via Hypothesis H) and further pointers, see:

Review:

In Chern-Simons theory

Since weight systems are the associated graded of Vassiliev invariants, and since Vassiliev invariants are knot invariants arising as certain correlators/Feynman amplitudes of Chern-Simons theory in the presence of Wilson lines, there is a close relation between weight systems and quantum Chern-Simons theory.

Historically this is the original application of chord diagrams/Jacobi diagrams and their weight systems, see also at graph complex and Kontsevich integral.

from Bar-Natan 1991

Reviewed in:

Applied to Gopakumar-Vafa duality:

  • Dave Auckly, Sergiy Koshkin, Introduction to the Gopakumar-Vafa Large NN Duality, Geom. Topol. Monogr. 8 (2006) 195-456 (arXiv:0701568)

See also

For single trace operators in AdS/CFT duality

Interpretation of Lie algebra weight systems on chord diagrams as certain single trace operators, in particular in application to black hole thermodynamics

In AdS 2/CFT 1AdS_2/CFT_1, JT-gravity/SYK-model

Discussion of (Lie algebra-)weight systems on chord diagrams as SYK model single trace operators:

  • Antonio M. García-García, Yiyang Jia, Jacobus J. M. Verbaarschot, Exact moments of the Sachdev-Ye-Kitaev model up to order 1/N 21/N^2, JHEP 04 (2018) 146 (arXiv:1801.02696)

  • Yiyang Jia, Jacobus J. M. Verbaarschot, Section 4 of: Large NN expansion of the moments and free energy of Sachdev-Ye-Kitaev model, and the enumeration of intersection graphs, JHEP 11 (2018) 031 (arXiv:1806.03271)

  • Micha Berkooz, Prithvi Narayan, Joan Simón, Chord diagrams, exact correlators in spin glasses and black hole bulk reconstruction, JHEP 08 (2018) 192 (arxiv:1806.04380)

following:

  • László Erdős, Dominik Schröder, Phase Transition in the Density of States of Quantum Spin Glasses, D. Math Phys Anal Geom (2014) 17: 9164 (arXiv:1407.1552)

which in turn follows

  • Philippe Flajolet, Marc Noy, Analytic Combinatorics of Chord Diagrams, pages 191–201 in Daniel Krob, Alexander A. Mikhalev,and Alexander V. Mikhalev, (eds.), Formal Power Series and Algebraic Combinatorics, Springer 2000 (doi:10.1007/978-3-662-04166-6_17)
from Narovlansky 2019

With emphasis on the holographic content:

  • Micha Berkooz, Mikhail Isachenkov, Vladimir Narovlansky, Genis Torrents, Section 5 of: Towards a full solution of the large NN double-scaled SYK model, JHEP 03 (2019) 079 (arxiv:1811.02584)

  • Vladimir Narovlansky, Slide 23 (of 28) of: Towards a Solution of Large NN Double-Scaled SYK, 2019 (pdf)

  • Micha Berkooz, Mikhail Isachenkov, Prithvi Narayan, Vladimir Narovlansky, Quantum groups, non-commutative AdS 2AdS_2, and chords in the double-scaled SYK model [arXiv:2212.13668]

  • Herman Verlinde, Double-scaled SYK, Chords and de Sitter Gravity [arXiv:2402.00635]

  • Micha Berkooz, Nadav Brukner, Yiyang Jia, Ohad Mamroud, A Path Integral for Chord Diagrams and Chaotic-Integrable Transitions in Double Scaled SYK [arXiv:2403.05980]

and specifically in relation, under AdS2/CFT1, to Jackiw-Teitelboim gravity:

In Dpp/D(p+2)(p+2)-brane intersections

from Sati and Schreiber 19c

Discussion of weight systems on chord diagrams as single trace observables for the non-abelian DBI action on the fuzzy funnel/fuzzy sphere non-commutative geometry of Dp-D(p+2)-brane intersections (hence Yang-Mills monopoles):

As codes for holographic entanglement entropy

From Yan 20

Chord diagrams encoding Majorana dimer codes and other quantum error correcting codes via tensor networks exhibiting holographic entanglement entropy:

From Jahn and Eisert 21

For Dyson-Schwinger equations

Discussion of round chord diagrams organizing Dyson-Schwinger equations:

  • Nicolas Marie, Karen Yeats, A chord diagram expansion coming from some Dyson-Schwinger equations, Communications in Number Theory and Physics, 7(2):251291, 2013 (arXiv:1210.5457)

  • Markus Hihn, Karen Yeats, Generalized chord diagram expansions of Dyson-Schwinger equations, Ann. Inst. Henri Poincar Comb. Phys. Interact. 6 no 4:573-605 (arXiv:1602.02550)

  • Paul-Hermann Balduf, Amelia Cantwell, Kurusch Ebrahimi-Fard, Lukas Nabergall, Nicholas Olson-Harris, Karen Yeats, Tubings, chord diagrams, and Dyson-Schwinger equations [arXiv:2302.02019]

Review in:

  • Ali Assem Mahmoud, Section 3 of: On the Enumerative Structures in Quantum Field Theory (arXiv:2008.11661)

Other

Appearance of horizontal chord diagrams in discussion of neutrino interactions in supernovae:

  • Duff Neill, Hanqing Liu, Joshua Martin, Alessandro Roggero: Scattering Neutrinos, Spin Models, and Permutations [arXiv:2406.18677]

Last revised on January 7, 2024 at 06:55:43. See the history of this page for a list of all contributions to it.

EditDiscussPrevious revisionChanges from previous revisionHistory (87 revisions) Cite Print Source